
 Wisp
Unification Theory - 5 Gravity
Wisp
Unification Theory - 5 Gravity
- Home
- About Me
- Reasons why Einstein was wrong
- One-way speed of light experiments
- Hot topic
- Q&A
- ACES - The end of Relativity

- Book Contents
- Introduction
- 1 Matter,Space and Time
- 2 Symmetry
- 3 Fractals
- 4 Wisp Space
- 5 Gravity
- 6 Electromagnetic Force
- 7 Wisp & S.R: Fundamentals
- 8 Wisp & S.R: Electrodynamics
- 9 Wisp & S.R: Doppler effect
- 10 Wisp & S.R: Relativistic Mechanics
- 11 Big bang
- Appendix A
- Appendix B
- Index A-Z
- Copyright
- Feedback
This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.
5
Gravity
Gravity is a phenomenon associated with the gravitational force acting
on any object that has mass and is situated within the Earth’s gravitational
field. But what causes it?
Newton was the first of the great scientists who had insight into its
true cause, although he never formalised proof of his idea. His law of
gravitation deals only with the dynamics of the problem, not its cause.
We shall see that wisp theory’s explanation of the cause of gravity
is similar to Newton’s thoughts. And using the concept of ‘zero-state
space’ reveals that objects are ‘pushed down’ towards the
Earth, not ‘pulled down’.
Einstein was also correct in saying that the curvature of space causes
the gravitational effect. It is the curvature of wisp space that creates
the radial compression force, which ‘pushes down’ on objects.
5.1 The weakest force
Of the four fundamental forces of nature – the gravitational force,
the electromagnetic force and the strong and weak nuclear forces –
gravity is the odd one out, and by far the weakest. Physicists have been
unable to integrate it successfully into their theories.
The ratio of the strength of the gravitational force to the electrical
force between two electrons, is the same as the ratio of the size of an
atom’s nucleus to that of the entire universe. The gravitational
force is so incredibly weak that it almost ceases to exist, and yet, its
effect spans the entire universe; and will one day determine its fate.
For two electrons, the ratio of gravitational to electrical force is:

We only feel the effect of gravity on the surface of the Earth, because
the gravity of the whole mass of the Earth – 6×10^24 kg –
is acting on us.
We are fortunate that most of the positive and negative electric charges
are neutralised within atoms, so we do not experience their true power;
if we did, we would be subjected to enormously powerful electromagnetic
force effects.
5.2 Current theories
The two theories that best explain gravity are Newton’s law of gravitation
and Einstein’s general theory of relativity:
5.2.1 Newton’s law of gravitation
This states that the gravitational force of attraction F between
any two masses m1 and m2
, whose centres are separated by a distance d, is given by the
equation
![]()
where G is the gravitational constant, which is a measure of the
strength of the gravitational force between two bodies and is usually
regarded as a universal constant.
Newton’s theory is simple and easy to understand. He introduced the
concept that gravitational force is ‘action at a distance’,
and so avoided having to explain how it propagates through space.
5.2.2 Einstein’s general theory of relativity
This is a complex theory, and applies to frames of reference that are
accelerating with respect to inertial frames. It builds on the principle
of equivalence: No experiment can distinguish between a uniform gravitational
field and an equivalent uniform acceleration.
Tests carried out to an accuracy greater than one part in a hundred million
million have shown that there is nothing to distinguish between gravitational
and inertial mass.
The theory predicts that mass and energy are responsible for the curvature
of space–time, and gravitational effects are a consequence of this.
The gravitational ‘force’ in this sense is regarded as fictitious.
In this space–time, light and material bodies follow paths of shortest
distance between points – geodesic lines. The rules of Euclidean
geometry breakdown – straight-line paths become curved; angles of
a triangle add to more than 180°; and the ratio of the circumference
to the diameter of a circle is less than pi.
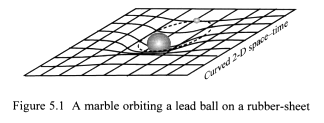
Figure 5.1 shows a simplified model: a heavy mass (lead ball) curving
two-dimensional space–time (rubber-sheet). This image helps us to
understand the process that causes the gravitational effect. However,
it only represents two-dimensional space–time which we view in three-dimensional
space. It is difficult to visualise what three-dimensional space–time
would look like.
The first success of Einstein’s theory was demonstrated by the correct
prediction of a small anomaly in the precession of the perihelion of the
planet Mercury – that Newton’s formula failed to predict –
of 43 seconds of arc per century.
Further tests confirm general relativity. In 1919 Arthur Eddington carried
out tests during a total solar eclipse and showed that light gets deflected
as it passes close to the surface of the Sun.
If Einstein’s general theory is the true explanation for the cause
of gravity, then it should be able to unify with quantum theory. But it
cannot, so some doubt remains as to whether general relativity is wholly
correct.
Its predictions are indeed remarkable. And many ideas from Einstein’s
theories are used in wisp theory – the main exception being the joining
of space and time.
5.2.3 Other theories
The standard model does not incorporate a theory of gravity, as it proves
too difficult to unify.
For gravity to be consistent with quantum and string theories, a force
particle called the graviton is predicted. It is thought to be responsible
for carrying force during gravitational interaction. It is predicted to
have zero rest mass and travel at the speed of light. However, there is
no proof that gravitons exist; their existence is only a theoretical assumption.
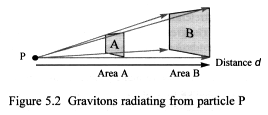
The graviton theory suggests that these particles emit from matter.
Figure 5.2 shows gravitons radiating from particle P, and passing through
area’s A and B. The density of gravitons in area B has been reduced
by a factor of 4, since area B is twice the distance from particle P than
is area A. As they radiate into space their intensity diminishes inversely
proportional to the square of the distance from P.
This is similar to Newton’s law of gravitation, in that the magnitude
of the force varies inversely proportional to the square of the distance
d – inverse-square law.
5.3 Wisp theory of gravitation
The gravitational force experience by matter is caused by its central
zero-state space interacting with radial compression forces in curved
wisp space. We will develop this idea in stages during this section.
Einstein’s general relativity says that the curvature of space–time
causes the gravitational effect. But in wisp theory, space and time are
not joined together and so time has no affect on curved wisp space.
5.3.1 Curved wisp space
Spherical matter-fractals force the surrounding wisp space to adopt spherical
symmetry or circular curvature. This forces wisps apart, stretching their
‘nuclear springs’, which creates tension force. The greater
the curvature, the larger the gaps, and the greater the energy stored
in curved wisp space.
Wisp space bends more acutely near matter, creating larger gaps, and becomes
rarer as a result. At greater distances the effect is reduced and wisp
space becomes denser, approach that of ‘flat space’ – see
section 2.2 (Face-centred cubic lattice).
Wisp space’s super-fine structure supports the principle of superposition,
whereby small individual effects of curvature due to many matter-fractals
are superimposed or added to give greater curvature effect. Therefore
curvature is proportional to the mass of a body.
5.3.2 Tension and compression forces
There are two types of force produced by curved wisp space: spherical
tension force and radial compression force.
Spherical tension forces are produced when wisp space curves around a
body (Figure 5.3). The forces equalise within spherical shells that surround
the body. And result because the presence of matter-fractals within the
body break the symmetry of flat one-state space, stretching it into spherical
shells. Spherical tension forces remain perpendicular to radial lines
projected from the body’s centre of mass P.
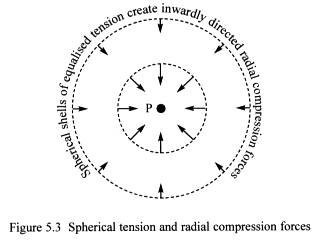
The effects of many spherical tension shells squeezing their enclosed
wisp space, produce the radial compression forces. Circular symmetry focuses
these towards the body’s centre of mass. And symmetry ensures that
even though the spherical tension forces create the radial compression
forces, the two remain orthogonal and have no component parts in each
other’s direction.
We examine the structure of the forces in more detail. Figure 5.4a shows
three wisps in flat wisp space. Their density is at maximum and strong
nuclear forces bind them together. There is no resultant force as radial
compression forces are absent, and any tension forces present cancel out.
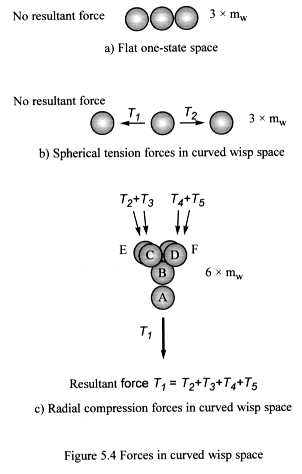
Figure 5.4b shows spherical tension forces in curved wisp space. They
follow the lines of curvature in wisp space and link together forming
closed loops of equalised tension – they form the contour lines of
a conservative field.
Figure 5.4c shows the radial compression force. Here wisp B plays a key
role in force distribution, by coupling the forces from particles C, D,
E and F, on to particle A, one large force is created from four smaller
ones. An important aspect of this coupling process is that it directs
the force along radial lines to underlying wisps and so strengthens the
orthogonal relationship between the two force types.
We could reverse the force arrows in the figure to show a large opposing
force splitting into four smaller ones. These smaller forces would further
reduce, spreading their effect uniformly throughout wisp space.
The radial compression force is created when matter distorts flat wisp
space. It is this force that is responsible for the gravitational effect.
The force that joins wisps together is the powerful nuclear binding force.
Curvature separates wisps by distances that would normally be considered
too small to be of any importance. But the powerful nuclear force magnifies
these tiny separations, enabling gravitational effects to be readily observed.
If we compare these to spring forces that obey Robert Hooke’s law,
then the value of spring stiffness would be extremely large. As a consequence
wisp space is very stiff. Small curvature produces large gravitational
effects, and larger curvature produces enormously powerful gravitational
effects.
The forces in the spring model and in wisp space vary according to the
inverse-square law, in agreement with Newton’s law of gravitation.
5.3.3 Force and the inverse-square law
A model showing springs connected to junction plates can be used to simulate
curved wisp space (Figure 5.5).
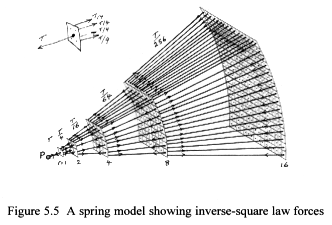
Consider the forces within a volume segment projected radially from
the surface of a body at point P. This volume is filled with springs and
identically sized junction plates. The plate boundaries are fixed at double
radius increments, i.e. 1, 2, 4, 8 and 16. A single spring connects to
the centre on one side of the plate and four identical springs connect
to the corners on the other side.
When placed under tension, the junction plates line up forming spherical
shells and the forces in the springs obey the inverse-square law –
doubling the distance from point P reduces the spring’s force by
a factor of four. The sum total of forces on the inside of the outer shell
is equal in magnitude to the single force T acting on P. The effects of
the force at P are therefore spread uniformly through the volume segment.
The springs in this example are being stretched, creating tension. But
equally, if the springs were compressed, they would still obey the inverse-square
law.
Now, comparing this spring model to curved wisp space. Imagine spherical
tension shells (junction plates) compressing the nuclear wisp springs
that lie along the radial lines. The force in the springs increases according
to the inverse-square law, and it is this force that is responsible for
the gravitational effect.
A small amount of energy is used in establishing forces in curved wisp
space – the principle of least action. This restores the order of
symmetry from one of disruption – caused by matter’s presence
– to that of circular symmetry. The energy is stored in curved wisp
space as gravitational potential energy.
In reality the distribution of spherical tension shells would be continuous
around P, and the splitting of forces would be smoothed out and not restricted
to specific shells. Wisp space gets stretched, but remains in a state
of static equilibrium.
Now, consider what would happen if the body were suddenly removed. Wisp
space would rush in and restore symmetry to that of flat wisp space.
If on the other hand we remove a thin layer of wisp space surrounding
the body – effectively isolating it – then it would be unable
to exert or feel any external force.
So we can conclude that the force responsible for the gravitational effect
comes from the surrounding curved wisp space and that it does not emanate
from the within the body.
5.3.4 Why obey the inverse-square law?
Forces do not have to obey this law; it depends on their environment.
For example, if we lived in a two-dimensional flat plane, wisps would
bend around ‘flat’ matter-fractals, following circular lines.
And since wisp gap size is proportional to the curvature of the arc of
a circle; and one arc is all that is needed for two-dimensional space,
the radial compression force would be proportional to the inverse of the
circle’s radius 1/r, and not its inverse squared.
For a spherical matter-fractal in three-dimensional space, two arcs are
required to represent curvature (curved surface area of a sphere). And
wisp gap size is obtained by multiplying the curvature of two arcs. So
the radial compression force is proportional to the inverse of the radius
squared, 1/r × 1/r.
If four-dimensional space did exist, then curvature would be obtained
by multiplying the curvature of three arcs. And the force would obey an
inverse cube law.
In fact, curvature has one dimension less that the space in which it exists.
Space has only three dimensions, and so radial compression forces must
obey the inverse-square law.
We have taken the first step in developing our gravitation theory by clearly
showing that forces in curved wisp space obey the inverse-square law.
But this wisp space is in a state of equilibrium, and we have yet to show
what effect this has on other matter-fractals placed in it.
Before going further, let us stop to reflect on Newton’s thoughts
as to the cause of gravity.
5.3.5 Newton’s thoughts
Newton published his mathematical work on gravity in his book Principia
Mathematica in 1687.
It was not necessary for Newton to know the cause of gravity in order
to develop mathematical laws describing its behaviour. But later, when
he published his treatise Opticks in 1704, he gave insight as to what
he thought caused gravity.
I believe Newton’s thoughts are correct and with the addition of
an interaction with matter-fractal’s zero-state space, the cause
of the gravity is revealed.

Sir Isaac Newton © Kim Albinson
In Query 21, Newton wrote on the subject of an ethereal medium link with
gravity.
- Is not this Medium much rarer within the dense Bodies of the Sun, Stars, Planets and Comets, than in the empty celestial Spaces between them? And in passing from them to great distances, doth it not grow denser and denser perpetually, and thereby cause the gravity of those great Bodies towards one another, and of their parts towards the Bodies; every Body endeavouring to go from the denser parts of the Medium towards the rarer?
In wisp space the gaps near bodies are greater than those further from
them. So wisp theory confirms Newton’s thoughts as to the cause of
gravitation, in that wisp space is rarer near bodies and denser further
away.
Even though the density variation is so small as to be almost non-existent
– similar to our comparison of the size of an atom’s nucleus
to that of the universe, its size is magnified by the strong nuclear force,
producing a macroscopic gravitational effect.
But there is something missing! We cannot produce the effects of gravitation
from density variation alone (Newton knew this). Matter placed in these
fields would experience a force that would be due to the difference in
density across its surface. And the resultant force would be proportional
to the inverse cube of the separation distance. So we cannot use this
concept as it stands, as we know the gravitational force varies as the
inverse square of the distance.
5.3.6 Wisp gravitational force
A spherical matter-fractal surrounding its zero-state sphere is placed
in curved wisp space (Figure 5.6). Spherical tension and radial compression
forces pass through the fractal’s layers, but cannot pass through
its ‘empty’ zero-state sphere. The effect of the ‘horizontal’
spherical tension forces cancel out by symmetry – equal and opposite
forces – and are not shown for clarity.
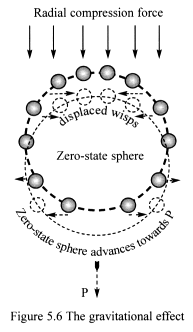
What happens when the radial compression force presses down upon the
matter-fractal?
Without rigid support from the fractal’s binding force, its ‘empty’
zero-state sphere would simply collapse, filling with wisps from curved
space – wisp space always tries to restore its order of symmetry.
But this does not happen, because the strong nuclear binding force rigidly
locks the fractal’s wisps around its ‘empty’ zero-state
sphere, preventing its collapse.
The radial compression force pushing down on the upper surface of the
matter-fractal’s zero-state sphere causes the gravitational effect.
The lower surface of the sphere cannot generate an opposing force, because
force cannot pass through ‘empty’ zero-state space. The radial
compression force is unopposed and is distributed on to the fractal’s
wisps. This causes the matter-fractal to accelerate downwards towards
P.
As the zero-state sphere moves towards P, wisps on its lower hemisphere
are displaced outwards at right angles to its direction of motion, and
close back in forming a new layer on its upper hemisphere.
Directly beneath the matter-fractal, a tiny ‘shadow’ forms,
because the downward acting force cannot pass through its zero-state sphere.
However, the chances of lower lying matter-fractals being caught in this
‘shadow’ are negligible. As the size of a matter-fractal’s
zero-state sphere is extremely small compared to the diameter of an atom
and the shadow is likely to have a short range.
5.3.7 Zero-state space shock waves
Along diagonal paths taken by high-speed particles, small shock waves
form as radial compression forces collapse the wisp space in their wakes
(Figure 5.7).
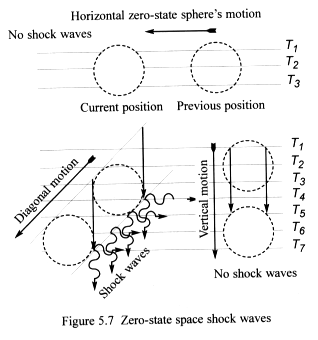
Matter-fractals that move horizontally through wisp space do so along
lines of equalised tension T, and consequently do not produce shock
waves. This is because the displaced wisps move horizontally around their
zero-state spheres maintaining constant tension.
Vertical motions of zero-state spheres do not produce shock waves either,
because the radial compression force at the top of the spheres never meets
up with the wisps beneath, as they are constantly blocked by presence
of zero-state space.
Only motions along diagonal lines through curved wisp space produce shock
waves. These occur because the radial compression force collapses the
wisp space in the wake of the matter-fractal’s fast-moving zero-state
sphere. The radial compression force pushes the upper part of the collapsing
wisp space into the lower part, knocking them together creating small
shock waves.
Fast-moving meteors descending diagonally towards the Earth will produce
small shock waves, which make contact with the Earth’s surface directly
beneath their paths. The shock waves are longitudinal pressure waves that
travel through wisp space at a speed of possibly ten times that of light.
5.3.8 Calculating gravitational acceleration
The radial compression force forms a vector field and its lines appear
to arise from infinity and terminate on any mass that can be regarded
as the source of the field.
At any point in curved wisp space the radial compression force Fr
varies proportionally to the mass of the source M, and inversely
to the square of the distance r from it. As shown by the equation
![]()
Spherical tension force produces the radial compression force that acts
on wisps, creating a downward radial compression vector pressure Pr.
Curved wisp space is unique in that it creates vector pressure (having
both magnitude and direction), unlike in liquids and gases where pressure
is scalar (having magnitude only, which acts equally in all directions).
Wisp space remains in static equilibrium, since equal and opposite forces
prevent wisp movements. Its wisps can be compared to bricks in the wall
of a tall building – they too can support huge pressures without
moving.
Imagine a matter-fractal with a solid centre being placed in curved wisp
space. Equal and opposite forces would pass through it, and it would remain
stationary. Its fractal shape would slightly distort under pressure, but
unless this was extreme (as around a black hole), the effect would be
negligible and can be ignored. However, we will discuss this effect later
– (Sections 5.6 Pioneers’ orbital discrepancies and 11.3.4 Star
speeds in rotating galaxies).
Now what happens when bricks are removed from the wall of our fictitious
building, creating a hole?
Prior to its collapse, the bricks at the base of the hole had no pressure
pushing down on them, whereas the bricks at the top of the hole were under
enormous pressure and began to crack. The wall collapses and bricks from
above fall into the hole.
Now consider what happens to our solid matter-fractal when its middle
is removed – creating a real matter-fractal complete with its zero-state
sphere (Figure 5.8)?
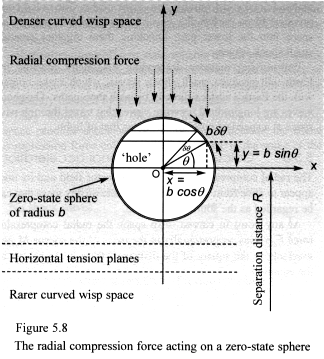
In curved wisp space it behaves in a similar way to the hole in the
wall, except that its structure does not collapse. Wisps lying at the
base of its zero-state sphere have no pressure pushing down on them, while
those on the upper surface experience pressure from the radial compression
force.
Gravitational acceleration calculations are shown in Equation set 5.1.
The centre of the matter-fractal is located at the x-y origin. We carry
out an integral that sums the effect of the radial vector pressure over
the upper zero-state hemisphere’s surface to get the total force
acting on the matter-fractal, which is its gravitational force. If we
then divide this by the matter-fractal’s mass we obtain its gravitational
acceleration.

We have to introduce a new constant W, which is similar to the
gravitational constant G – it has the same numerical value
but different units.
This model accurately predicts gravitational acceleration for matter-fractals
– fundamental particles – of any size. On the surface of the
Earth its value is 9.8 m/per sec per sec. However, there is one important
condition imposed:
- The masses of the matter-fractals must be proportional to the surface area of their zero-state spheres, i.e. the square of their radii, b.
If the masses of the matter-fractals were to vary in the conventionally
manner – as the cube of their radii – then the equivalence
principle established by Einstein would be violated. However, if a
number of atoms made from these matter-fractals were assembled together
to make a large homogeneous isotropic body, then the mass of that body
would be proportional to the cube of its radius as expected.
Physicists have carried out tests to an accuracy of 1 part in 10^14 and
shown that there is no detectable difference in the inertial and gravitational
mass for different substances. To detect a difference using modern methods
the zero-state radius would need to be at least one hundred times larger
than an atom. The formula shows that for zero-state radii on subatomic
scale, the difference in acceleration between different sized particles
is far too small to be detected at present.
So far, we have dealt with the gravitational effect of a matter-fractal
in curved wisp space. It should be noted, however, that the matter-fractal
would also superimpose its curvature of wisp space on the body P, resulting
in both bodies accelerating towards each other with equal and opposite
forces.
We have not included any relativistic effects in gravity, so as to avoid
over-complicating matters.
5.3.9 Bending light
The curvature of wisp space by matter or energy will affect the path of
light. Light is a pattern of oscillating transverse wisp waves, which
lack zero-state spheres. Even though they do not possess zero-state spheres
they are affected by gravitational force, and their paths will follow
the curvature of wisp space.
5.4 Podkletnov’s experiments
5.4.1 Gravity shielding
There have been some very interesting developments with experiments concerning
gravity shielding.
In September 1996 a report of an experiment performed by Eugene Podkletnov
was about to be published by the Institute of Physics, London, in their
Journal of Physics D: Applied Physics, but was suddenly withdrawn
by Podkletnov. Possibly because commercial backers wanted the discovery
kept secret or the Tampere University of Technology in Finland, where
he worked, feared loss of credibility. Whatever the reason is, doubt still
remains as to whether this discovery is genuine.
Scientists at the University claimed they had discovered by accident a
gravity shielding effect, while carrying out routine research work on
superconductivity. They discovered that objects suspended above a cryostat
containing a spinning superconductor disc could lose up to 2 per cent
of their weight (Figure 5.9). The effect penetrated the floor above the
laboratory, but not beneath the device.
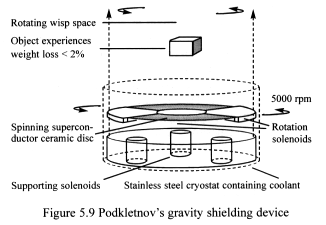
The scientists used a spinning ceramic superconductor toroidal disc
of composite structure – 275 mm across and 10 mm thick – suspended
in a magnetic field and enclosed in a low-temperature container called
a cryostat. Liquid nitrogen and liquid helium vapours were used to cool
the disc to around 40 K. The upper layer of the disc became superconducting,
whilst the lower layer stayed resistive. High-frequency currents were
applied to the solenoids causing the disc to lift and rotate.
On first hearing about the experiment, I thought it plausible that such
an effect could occur if wisp space were made to rotate at high-speed.
And it would only be a matter of time before further news on the subject
followed.
The mass of the Earth curves wisp space slightly, and this creates the
gravitational force. But when wisp space rotates, centripetal forces stretch
the horizontal spherical tension forces moving the wisps further apart.
This reduces the curvature and hence the gravitational effect.
Since the disc is small and the curvature of wisp space at the Earth’s
surface is very small, we can compare the rotation effect to that of bob
weights on a spinning governor. They move outward as rotation speed increases
and this reduces curvature. The reduction in gravity is related to the
disc’s size and its rotation speed. And somehow, the high-frequency
electromagnetic fields generated by the device interact with the disc’s
crystal structure causing wisp space to rotate. The spinning motion of
the disc magnifies the effect.
Scientists are having great difficulty in trying to repeat this experiment
because of secrecy of information. The difficult part is possibly trying
to get wisp space to rotate.
Ron Koczor, head of a group at NASA’s Marshall Space Flight Center,
Huntsville, Alabama, has invested $600,000 in building a replica of Podkletnov’s
apparatus. Hopefully they will get a positive result soon.
Boeing, the world’s largest aircraft manufacturer, is also interested
in the work. Their researchers in Seattle are trying to develop gravity
propulsion devices.
If results prove positive, then the effects produced by these small devices
would violate Einstein’s general theory of relativity.
5.4.2 Impulse gravity generator
In an article published in New Scientist, 12 January 2002, Podkletnov
claimed to have made a device that produces a pulse that has the same
properties as a gravitational field. The pulse can pass through a steel
plate and knock over a book placed on a table one-kilometre away.
Wisp theory predicts this effect is also possible, simply by rotating
wisp space horizontally instead of vertically.
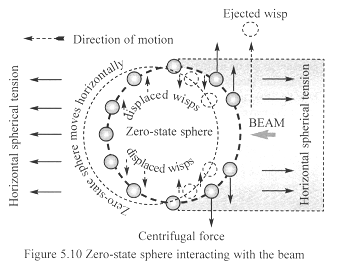
Figure 5.10 shows the horizontal beam acting on a matter-fractal placed
in its path. Centripetal forces that develop in the rotating beam cause
its wisps to move outwards, reducing the beam’s density. Earth’s
spherical tension force pulls horizontally on one side of matter-fractal’s
zero-state sphere, but the ‘equal and opposite’ tension force
pulling on the other side is reduced because the beam’s density is
lower. This causes a net force to act on the zero-state sphere, which
causes the matter-fractal to repel from the beam’s source. This explains
why the book experienced a repulsive impulse force, causing it to fall
over.
Some of the beam’s energy will be absorbed by the steel plate and
air particles in its path. But the magnitude of force exerted by a horizontal
beam would be much greater than that force cause by a vertical beam.
Again, secrecy shrouds the experiment and it has not been verified. But,
wisp theory predicts that if the original gravity ‘shielding’
effect is possible, then the impulse beam effect is also possible. It
is possibly the original ‘vertically operated’ device, modified
and placed on its side, projecting a horizontal beam.
The commercial potential for the impulse beam would be vast, explaining
why both NASA and Boeing are taking these reports seriously.
5.5 Quantum gravitational effects
We have looked closely at the gravitational effects that take place at
the centres of the fundamental particles. The gravitational effect arises
from the radial compression force causing pressure to act on matter-fractal’s
zero-state upper hemisphere.
Quantum theory is amazingly successful and adapts perfectly to the structure
of wisp space. Wisp space’s transverse waves cause the wave patterns
of quantum theory.
Quantum mechanics does fully explain the behaviour of a particle’s
bound states in a gravitational field. But I do not believe it is necessary
to explain gravity in terms of quantum theory’s force particle –
the graviton. And it is not necessary to use the theory to explain the
cause of gravity.
5.6 Pioneers’ orbital discrepancies
The first spacecraft to explore the planets in the outer solar system
were the Pioneers 10 and 11, launched in 1972 and 1973 respectively. After
successfully completing their missions they drifted out of the solar system
in opposite directions, journeying on towards the stars.
John Anderson and other scientists at NASA’s Jet Propulsion Laboratory
have discovered that an unexpected tiny deceleration force (less than
a nanometre per second per second) has affected both spacecraft.
According to Newton’s law of gravitation, only the weakening gravitational
pull from the receding Sun should slow them down. But Pioneer 10’s
position is some 400,000 km behind schedule, indicating that an additional
decelerating force has affected it.
Wisp theory predicts an additional tiny deceleration force directed towards
the Sun. This occurs because curvature reduces the density of wisp space.
At a greater distance from the Sun, wisp space is denser – closer
to one-state space.
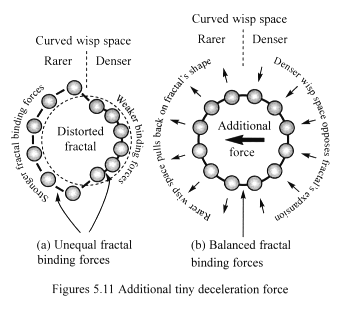
Figures 5.11 shows the effect this has on a matter-fractal’s structure. As it moves away from the Sun, it experiences the expected Newtonian gravitational force – due to the radial compression force. But variation in the density of curved wisp space causes the fractal’s shape to distort (Figure 5.11a), becoming larger in the rarer space facing the Sun. The figure’s pear-shaped distortion has been greatly exaggerated to show this effect. The fractal’s binding force acts to restore spherical symmetry and in doing so creates opposing push–pull forces in the surrounding wisp space (Figure 5.11b). Both the Newtonian gravitational force and the additional retarding force act in the same direction – towards the Sun.
5.7 Gravity Probe B
NASA are planning to launch the Gravity Probe B spacecraft to test two
as-yet untested predictions of Einstein’s general theory of relativity.
It will test for the effect of frame dragging – space dragged around
by the Earth’s rotation – and geodetic precession.
The experiment will use four small, incredibly precise gyroscopes to help
detect the small relativistic effects around the Earth. The frame dragging
effect will cause a small force to push the gyroscope’s spin axis
out of alignment, as it orbits the Earth. And the much larger geodetic
effect – warping of space–time – will also affect the gyroscope’s
spin, but in a direction that is perpendicular to that of the frame dragging;
and so the effects can be measured separately.
It seems plausible that large bodies of spinning matter could drag space
around. The movement of wisp space around a body would increase its circular
curvature on its equatorial plane and flatten the curvature at the poles.
These effects are likely to be extremely small around the Earth.
5.8 Conclusion
There have been no major changes to our understanding of gravity for the
past 300 years. Newton’s law of gravitation gave scientists great
opportunity to develop new ideas. So accurate was his theory that it is
still widely used today. Scientists used it to calculate the small error
in precession of Mercury’s orbit, and this prompted a search for
a better theory. But Newton’s theory has not failed, it has merely
been replaced by a theory that gives more accurate results – Einstein’s
general theory of relativity.
Wisp theory combines a unique property of matter – zero-state space
– with both Newton’s and Einstein’s ideas, to form a new
theory of gravity.
I believe that Einstein’s success with gravity arose from his ideas
on curved space coupled with relativistic time dilation effects. Wisp
theory supports these views, but does not agree that space and time are
joined, and so differs fundamentally from Einstein’s theory.
Wisp theory treats gravity as a force, a view held by Newton but not by
Einstein. But most important is that the source of gravity is the radial
compression force that passes through space by contact with neighbouring
wisps. It is not caused by ‘action at a distance’ requiring
no medium to transmit it. Einstein believed that the gravity force is
fictitious – a consequence of curved space–time.
Wisp theory supports Newton’s views as to the cause of gravity. Although
its effects propagate through wisp space at the speed of light –
a prediction of Einstein’s general theory of relativity – and
not at infinite speed, as Newton had supposed. However, most scientists
believe that Newton’s law of gravitation applies to the entire universe.
And for slow-moving systems Newton’s theory appears correct. It only
begins to suffer when speeds in the system increase and relativistic effects
come in to play.
Wisp theory predicts that the rotation of wisp space produces additional
gravitational effects. And if reports of Podkletnov’s gravity experiments
are true, which I believe they are, then a new era in science is about
to begin.
Home --
About Me -- Reasons
why Einstein was wrong -- One-way
speed of light experiments -- Hot
topic -- Q&A
-- ACES
- The end of Relativity --
Book Contents -- Introduction
-- 1 Matter,
Space and Time -- 2
Symmetry -- 3
Fractals -- 4 Wisp Space
-- 5 Gravity -- 6
Electromagnetic Force --
7 Wisp & S.R: Fundamentals
-- 8 Wisp & S.R: Electrodynamics
-- 9 Wisp
& S.R: Doppler effect -- 10
Wisp & S.R: Relativistic Mechanics --
11 Big bang -- Appendix
A -- Appendix B -- Index
A-Z -- Copyright -- Feedback