Wisp Unification Theory - 4 Wisp Space

• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

4

Wisp Space

Here we will see our perception of reality reverse. What we think of as ‘emptiness’ is in fact full of ‘ether’ particles called wisps (weightless one-state particles). And what we think of as solid is created by their absence. What we think of as ‘normal flat space’ or ‘void’ occurs when wisp packing is at its maximum.
The idea of an ether medium is not new. So why now should an ether theory be taken seriously? Well, it gives the right answers; it matches special relativity’s predictions; and it gives a simple answer to the question ‘What causes gravity?’

4.1 Wisp space’s structure

4.1.1 States of space
Wisp space is in a state of being either empty or full, or in an intermediate state. For example:

• Empty space contains nothing, and wisp theory refers to it as
  ‘zero-state space’. It has no energy and does not transmit force. It does, however, play a key role in creating matter and three of the four fundamental forces of nature.
• Full space is densely packed with wisps and is referred to as
  ‘one-state space’ or ‘flat space’. The strong nuclear force binds wisp together – the only force of nature that exists as a real property of the wisp. Wisps can move in one-state space, but generally remain fixed within its lattice structure.
• Intermediate-state space is a combination of one-state and
  zero-state space. This creates regions with diverse properties such as: matter-fractals, curved space, magnetism, gravitational compression and tension forces, and electric charge.

4.1.2 Wisps
Wisps are the smallest fundamental particles in nature. They have specific size and mass. Although they possess mass, they are unaffected by gravitational force since the gravitational effect is caused by curved wisp space and does not exist as a separate substance. No antiwisp particle exists.

4.1.3 Matter-fractals
Wisp theory is an ether theory with a unique property – matter-fractals, which I believe, form the fundamental particles of nature – the quarks and leptons.
Spherical fractal structures form within wisp space around regions of zero-state space (‘empty’ zero-state spheres). Gaps appear between neighbouring wisps as they wrap around the zero-state sphere. The gaps stretch the strong nuclear binding force, and this gives the fractal structure enormous strength. Once formed, the matter-fractal is able to move effortlessly through wisp space, since equal and opposite forces form across its surface. As it moves, wisps are displaced, creating transverse wave patterns – quantum waves.
Figure 4.1 shows a cross-section view of a matter-fractal. Its scale is not proportional to the wisp’s size, as many millions more would be required to form each structure.

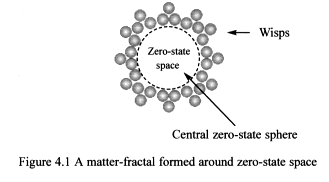
A matter-fractal’s size is dependent on the radius of its central zero-state sphere. This is crucial in determining the type of fundamental particle formed. Since matter-fractals form around the surface of zero-state spheres, a particle’s mass is proportional to the surface area of its zero-state sphere, and its density will vary inversely proportional to the distance from the sphere. The thickness of a matter-fractal’s layers is proportional to its zero-state sphere’s radius. A specific number of wisps get locked into its structure, giving it its unique mass.
The formation of matter-fractal structures is based upon simple processes that utilise the principle of least action – wisp movements are minimised while the fractal shapes adjust for maximum stability. As stated earlier, it would be almost impossible to use conventional mathematics to calculate the fractal patterns, since the numbers of wisps involved is too high. The use of cellular automata could provide the answer. Instead of solving complex mathematics, computers running automata programs might determine which fractal patterns form in wisp space. Patterns that produce best stability for lease movement could then be selected for comparison with the known masses of the fundamental particles.
The ‘stretched’ strong nuclear force gives the fractal structure extra strength, allowing it to move effortlessly through wisp space and survive small collisions. However, if the matter-fractal gets too large, it becomes unstable and can quickly break up into smaller more stable structures. Larger fractal structures are more prone to break during high-speed collisions.
Figure 4.2 shows a matter-fractal stationary in wisp space. Its presence breaks the symmetry of flat one-state space. One-state space is forced to wrap around the fractal structure, but it does not have the strength to break it.

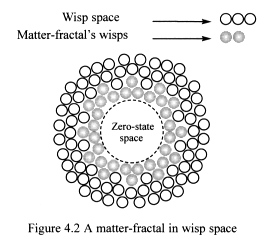
As matter-fractals move, they displace wisps – transverse displacement – to either side by the actions of equal and opposite forces, creating quantum wave patterns in wisp space. Only the matter-fractal’s shape is preserved as it moves through wisp space; the wisps that form it are continuously replaced.
A few months after I discovered this property of matter, I asked my wife to explain to me what she understood about this new idea. She replied ‘Matter is particles of nothingness.’ She is right, without nothingness (zero-state space) matter would not exist.

4.2 Early ether theories

4.2.1 René Descartes
The seventeenth century philosopher and mathematician René Descartes thought that the universe was filled with small invisible particles or ‘corpuscles’ that moved effortlessly in whirlpool vortices. Opaque matter floated in this medium and was caught up by the whirlpools. Once started, their motions would continue and the energy in the universe would stay constant.

4.2.2 James Clerk Maxwell
In 1856 James Clerk Maxwell showed that an incompressible fluid behaved the same way as the fields that produce magnetic and electric effects. In his model, magnetism is caused by vortices in the fluid and electric current contained in fluid cells.
With elasticity added to his model, in 1864 he developed the fundamental equations of electromagnetism and found that transverse electromagnetic waves could move at the speed of light through the hypothetical ether medium.
Maxwell discovered that electromagnetic waves possessed magnetic and electric fields that oscillated at right angles to each other and to the direction of wave propagation. It was difficult to imagine how a fluid could produce these effects, and so the link between his equations of electromagnetism and the ether was lost.
Maxwell developed his theory on the basis that electromagnetic fields transfer force from one point to a neighbouring point, in a field that has properties that may be likened to an elastic fluid. Yet his equations of electromagnetism are purely mathematical in nature and have no direct link to a fluid medium. His work certainly supports the existence of the ether, but it does not prove it exists; more proof is needed.

4.2.3 J.J. Thomson
Sir Joseph John Thomson carried out an analysis of vortex rings in 1883 and theorised that atoms might be vortex rings within the hypothetical electromagnetic ether.

4.2.4 Michelson and Morley
An experiment conducted in 1887, by Albert Michelson and Edward Morley, to measure the velocity of the Earth through the ether, gave good reason to believe that the ether did not exist. If it did, then surely the motion of the Earth through it would give a positive result, but it gave a negative result – zero!
The pressure was on to explain the findings of the experiment or simply dismiss the notion of the ether.

4.2.5 Insufficient proof
There is no direct proof that the ether does or does not exist. Current theories tend to dismiss it rather than include it.
Wisp theory is built upon wisp space – a type of ether medium, which is responsible for creating particles and transmitting force between them. Without it force would not propagate. Later we will see that it is the inability of force to transmit through zero-state space ‘emptiness’ that causes the effect of gravitation.
Proof of the existence of the ether requires abandonment or major modification to Einstein’s special theory of relativity, and an explanation to why the Michelson–Morley experiment gave a null result. A revised relativity theory and an explanation are given by wisp theory.

4.3 Waves in wisp space
Two types of travelling wave are associated with motion through wisp space: transverse waves and longitudinal waves. As they move through wisp space, wisps are displaced in transverse and longitudinal directions respectively, and their respective wavelengths are lambda t and lambda l. They share properties commonly associated with waves: diffraction, reflection, and refraction.
By way of analogy, we can compare them with water waves: Ripples (transverse waves) moving across the water’s surface are like electromagnetic waves or matter-fractal’s quantum waves. And sound waves (longitudinal waves) that travel through water are like longitudinal waves that travel through wisp space.
Just as sound waves in water travel much faster than surface ripples, so we can expect wisp longitudinal waves to travel faster than wisp transverse waves. The fastest transverse wave in wisp space is light, so wisp longitudinal waves should travel faster than light!

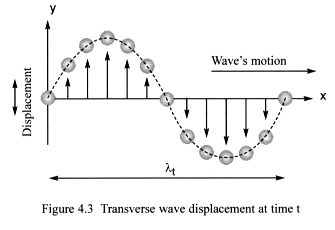
4.3.1 Transverse waves
As they travel through wisp space they displace wisps in directions that are at right angles to the wave’s motion (Figure 4.3), and wave speeds are less than or equal to light-speed through wisp space. Types include: matter-fractal’s quantum waves, electromagnetic waves, gravitational waves, and de Broglie waves – first proposed in 1924 by Louis de Broglie.

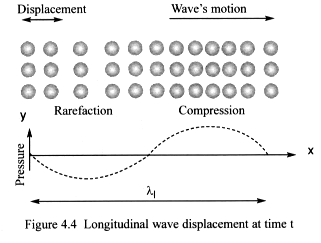
4.3.2 Longitudinal waves
Displacement takes place in the same direction in which the wave travels – similar to sound waves travelling through air or water (Figure 4.4).
The front half of the wave compresses wisp space as it passes through it. This is followed by a half cycle of rarefaction, which stretches wisp space. Pressure and density changes that occur in wisp space are incredibly small, but the wave speed is very fast – possibly ten times the speed of light.
Wisp theory predicts the existence of faster-than-light longitudinal waves, but this is a new concept and scientists have no knowledge of it. These waves are responsible for meteors’ shock waves (discussed later), longitudinal gravitational waves (following supernova events) and possibly quantum entanglement.

4.3.3 EPR Paradox
Longitudinal waves that travel faster than the speed of light may offer an explanation for the strange findings of quantum entanglement.
In 1935, Einstein, with support from Boris Podolsky and Nathan Rosen, proposed a thought experiment referred to as the ERP Paradox. If Einstein were right then quantum theory would be incomplete.
Consider an example where two subatomic particles interact and are moved a great distance apart. The particles are correlated so that the action of one affects the behaviour of the other. When measurements are made simultaneously on the separated particles, the results should be independent of each others quantum state; since they cannot share information, as it would need to travel between them at a speed greater than that of light.
Experiments carried out to test this proposal have proven Einstein wrong. It appears that separated particles remain entangled and do somehow communicate their information at speeds faster than that of light. Einstein referred to this as ‘spooky action at a distance’, and quantum mechanics argue that these states are non-local and so there is no paradox! But if information is communicated at a speed faster than light, does that not undermine special relativity’s claim that nothing travels faster than light?

4.4 Matter-fractal’s motion through wisp space
As transverse waves travel through wisp space, the wisps are moved from side to side, they do not travel along with the wave. The wave carries only its shape, energy and momentum.
A matter-fractal travels through wisp space as a transverse wave packet. Wisps that make up the matter-fractal play a similar role to wisps that make up a transverse wave’s shape, only here the matter-fractal’s shape is much more complex. As the matter-fractal travels through wisp space, a series of equal and opposite forces move wisps in directions that are at right angles to the matter-fractal’s direction of motion. All wisps are displaced by the matter-fractal and none travels along with it. Matter-fractals carry fractal shape, energy and momentum.
Transverse wisp displacement can be interpreted mathematically as a Fourier series that forms the wave functions of quantum mechanics. By way of analogy, a circle can be constructed from the points of intersection of an infinite number of tangent lines. But that does not mean that all circles must have an infinite number of tangents attached to them. Similarly we can represent a matter-fractal as an infinite number of sine waves forming a quantum wave packet. But that does not mean that matter-fractals are made from sine waves. It is just that their behaviour in wisp space can be modelled by an infinite number of waves summed together to form a wave packet, since matter-fractals replicate these patterns as they travel through wisp space.
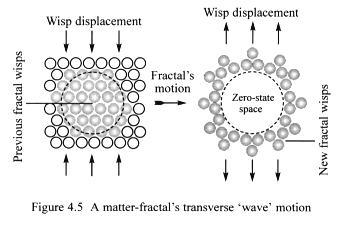
Figure 4.5 shows wisp space displacement resulting from matter-fractal’s motion. Note that the wisps that previously made up the fractal have returned to their original positions, and new wisps now form the matter-fractal’s pattern.
Matter would be unable to move through wisp space as a transverse wave packet if it did not possess zero-state space. This is needed to form stable matter-fractal structures.

4.5 Absolute frames of reference
A single absolute frame of reference is an abstract notion that in practice does not exist.
Any frame of reference in which wisps are stationary can for practical purposes be considered as absolute. It is theoretically possible for several absolute frames of reference to be in relative motion, so long as they are physically isolated. Otherwise they would combine to form a single absolute frame.

4.5.1 Local absolute frames of reference
It is likely that between any two local frames – separated by a great distance – there may be a small relative motion between them caused by movement of wisp space. It is perfectly reasonable to consider both local frames as absolute in their own right and so ignore negligible relative motion effects.

4.6 Newton’s laws of motion
At speeds much less than light speed, matter-fractals move through one-state space according to Newton’s three laws of motion. These laws of motion are as follows:

4.6.1 Newton’s first law of motion
A body continues in a state of rest or uniform motion in a straight line unless it is acted upon by external forces.

At rest a matter-fractal is stationary in an absolute one-state space. There is no motion whatsoever between the fractal and the surrounding wisps, so quantum waves are absent.
When a matter-fractals moves through one-state space, it displaces wisps at right angles to its motion – transverse wave motion displacement – creating quantum wave patterns. There are no friction forces acting to slowing it down – wisp space is inviscid (frictionless). Equal and opposite forces establish across its surface allowing it to move effortlessly through wisp space in accordance with Newton’s first law of motion.

4.6.2 Newton’s second law of motion
The rate of change of momentum of a moving body is proportional to and in the same direction as the force acting on it, i.e. F = d(mv)/dt, where F is the applied force, v is the velocity of the body, and m its mass. If the mass remains constant, F = mdv/dt or F = ma, where a is the acceleration.

When force acts on a matter-fractal it causes distortion to its shape. But because its shape is held together by the nuclear binding force, it is able share the effect of the applied force among all wisps in its fractal structure. These wisps have inertia and react by accelerating in directions at right angles to the bodies motion; the quicker they move the faster the matter-fractal shape moves.

4.6.3 Newton’s third law of motion
If one body exerts a force on another, there is an equal and opposite force, called a reaction, exerted on the first body by the second.

We would expect forces acting between particles to be equal and opposite, and this is always the case in wisp theory.
However, there is one surprise, due to the fact that in wisp theory transverse force transmits at the speed of light. The effect of force on particles travelling at near-light speed reduces. This makes it harder to speed up and slow down fast-moving particles. We cover this later (Sections 7.14.2 accelerating subatomic particles and 7.14.3 decelerating subatomic particles).