• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete chapter. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

10

Wisp and Special Relativity: Relativistic Mechanics

10.1 Conservation of momentum
We use wisp’s velocity transformations to calculate the momentum before and after an elastic collision between two identical particles of masses ma and mb.
Particle A is stationary in absolute rest frame S, and particle B is stationary with respect to moving frame S’. Frame S’ moves through wisp space at speed V along the negative x-axis.
Both particles receive a push along their y-axes, which move them towards each other at equal speeds, and they collide at a point that is the origin of both of their reference frames.
Figure 10.1 shows how each observer sees the event prior to the collision. Both observers agree that the particles approach each other at equal speeds in their y-axes.

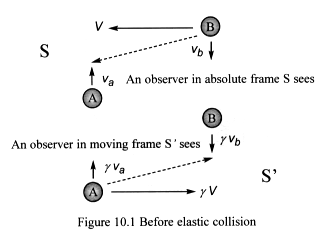
Figure 10.2 show the particles strike each other with a glancing blow, leaving their speeds in their x-axes unchanged.
We ignore the force and jiggle dilations that affect the electrostatic forces within the particles, as they have no affect on the outcome of the collision.

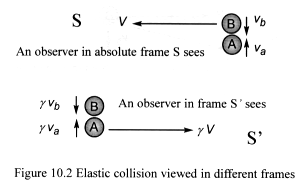
The observer in frame S sees both particles bounce off each other without losing speed.
After applying the rules for time dilation compensation (Section 7.15.4), the moving observer in frame S’ sees a similar collision process, except that all observed speeds are increased by gamma.
Equation set 10.1 shows the equations for proving the conservation of momentum in both frames.

The value of momentum in frame S is absolute, and the value in the moving frame S’ is relative – not real in an absolute sense. But as far as the moving observer is concerned, all physical processes that take place appear real enough, and the law of conservation of momentum is upheld.
We have ignored the small additional relativistic effects caused by the particles’ motions in the y-axis, as they are too small to be significant.
Each observer records a different time interval for the collision. Let T be the time interval from the moment particle A is pushed to the moment it returns to its start point on its y-axis, and T’ be particle B’s time interval when measured in frame S’.
The moving observer (frame S’) sees the whole collision process speeded up (rules for time dilation compensation) and so the observer’s time interval T’ will be correspondingly shorter by a factor of gamma. (Only when observers carry out identical experiments in their local frames will they agree on results.)
The observers witness a collision process that is different from that predicted by special relativity, because mass is invariant in wisp theory.
Special relativity predicts that each observer sees the faster moving particle’s mass increase as a consequence of relative motion. And the time interval from push to collision and return for the faster moving particle (Particle B in frame S, and particle A in frame S’) is longer by a factor gamma. The faster moving particle travels slower in its respective y-axis and so, in order to comply with the conservation of momentum, the faster moving particles’ mass must increase by a factor of gamma.
In wisp theory, each observer records the particles’ y-axes speeds to be the same and the masses of the particles do not change.

10.2 E = mc^2
The discovery by Einstein that mass and energy are equivalent, E = mc^2, is a remarkable prediction on the part of special relativity. Energy creates particles and particles change into energy.
We will look at this in detail and try to understand exactly what the implications are from wisp theory’s perspective, bearing in mind that wisp theory states that mass is invariant – it does not increase with a body’s speed. But what is the connection?
First we need to derive a mathematical relationship between energy and mass, which we do by calculating the energy required to move a force over a distance – in absolute wisp space (Equation set 10.2).

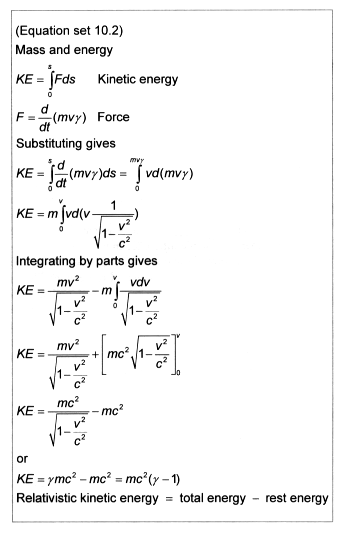
The value for kinetic energy is the same as that discovered by Einstein, but there is a subtle difference in wisp theory’s interpretation. When a body is stationary in wisp space, its kinetic energy is zero, but it has a fixed amount of rest energy. This is the energy that was stored when the body formed, pulling one-state space apart to create zero-state spheres. A zero-state sphere’s surface area is proportional to its surrounding fractal’s mass, and the energy used to create it is stored as nuclear ‘spring’ potential energy (rest energy) within the structure of its matter-fractal. This is the mc^2 component and it stays at a constant absolute value as the body moves through wisp space.
The (gamma * mc^2) component is the total energy acquired by the body as it moves through wisp space. The gamma term results from the effect of force dilation on the body, which creates a quasi-mass increase – see section 7.14.1 (Relativistic mass increase: quasi-mass).
The force used to create matter-fractals is the same as that which cause them to move – increasing their kinetic energy, so we would expect there to be a direct relationship between the two energy types responsible for the force – potential and kinetic, which is why mass and energy are equivalent.
The relativistic kinetic energy is the total energy minus the rest energy. We find that for small speeds through wisp space this reduces to the classical expression for kinetic energy (Equation set 10.3).

10.2.1 Energy into mass
Small particles travelling at near light speed in particle accelerators can create more massive particles during collisions. But how does kinetic energy cause a particle with a heavier mass to form, if the small particles’ masses do not increase as they speed up?
Consider two small particles, each approaching the other at an absolute speed of 0.99c (Figure 10.3). Their combined mass before the collision is 2m.

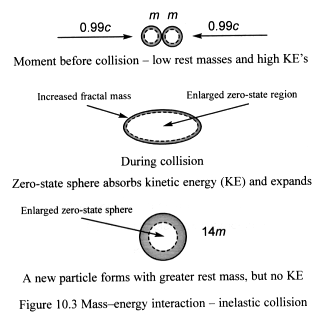
During collision the particles stick together, forming one large expanded region of zero-state space. This happens because the particles had large kinetic energies and during the collision their zero-state spheres merged and stretched, absorbing the particles’ kinetic energy and forming a larger region of zero-state space. This enlarged region quickly reshapes forming a particle of larger mass, 14m. (A huge amount of energy is stored as strong nuclear potential energy – rest energy – in the matter-fractal’s structure that surrounds its zero-state sphere).
Typically this larger particle would be unstable and short-lived. It could resonate, break apart, and even release the same small particles that created it.
The recently discovered top quark is about 40,000 times more massive than the more common up-quark. Wisp theory states that their masses are proportional to the square of their zero-state spheres’ radii, which makes the top quark about 200 times bigger than the up-quark, explaining why it is very unstable.
In general the size of matter-fractal’s zero-state sphere is minute, almost point-like, in comparison to the size of an atom’s nucleus.

10.3 Conservation of charge
The magnitude of the total electric charge of a system of particles before and after a high-speed collision is conserved.
Charge arises from asymmetry or twists in the structure of matter-fractals. And it follows from Newton’s third law of motion that equal and opposite amounts of twist must be created or destroyed in wisp space when charged particles are created or destroyed.
By way of an analogy, think of stretching an elastic band by applying equal and opposite force to its ends. Pulling one end only does not stretch it. A similar process applies with newly created charged particles; they can only be made if wisp space twists in equal and opposite ways.
This explains why quarks (asymmetric matter-fractals) can only appear in pairs with opposite charge following collisions.