Wisp Unification Theory - Appendix B

• Home
• About Me
• Reasons why Einstein was wrong
• One-way speed of light experiments
• Hot topic
• Q&A
• ACES - The end of Relativity

• Book Contents
• Introduction
• 1 Matter,Space and Time
• 2 Symmetry
• 3 Fractals
• 4 Wisp Space
• 5 Gravity
• 6 Electromagnetic Force
• 7 Wisp & S.R: Fundamentals
• 8 Wisp & S.R: Electrodynamics
• 9 Wisp & S.R: Doppler effect
• 10 Wisp & S.R: Relativistic Mechanics
• 11 Big bang
• Appendix A
• Appendix B
• Index A-Z
• Copyright
• Feedback

This page contains the complete appendix. To download the new 2011 2nd edition of wisp unification theory go to the homepage.

Appendix B

Fizeau’s Experiment

In 1851 Armand Fizeau performed an experiment to measure the speed of light in moving water. Its purpose was to measure the value of the ether drag coefficient.
He discovered that changes in the speed of light are proportional to the water’s flow rate, and he calculated the drag coefficient to be 0.48, a result consistent with Fresnel’s earlier prediction of 0.43.
However, it turned out that the drag coefficient predicted by Fresnel gave a result that appears correct, but its derivation is not wholly correct.
We know that moving water does not drag wisp space along with it, but there is some merit in Fresnel’s thought process. Both Einstein and Fresnel have produced equations that appear to give correct predictions for the speed of light moving through water, and we shall apply wisp’s velocity transformations to both sets of established equations.
Wisp theory will show that there is a small difference in predicted values caused by the Earth’s motion through wisp space.

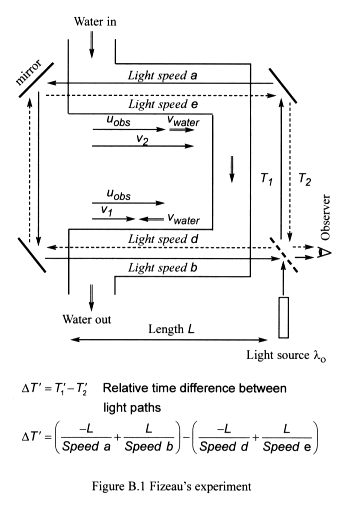
B.1 Apparatus
Light of fixed wavelength emits from a source and strikes a half-silvered mirror that splits it into two rays, which travels along different paths – with and against the flow of water (Figure B.1). We draw the rays separated for clarity to allow their individual speeds to be seen, but in reality they would form a single ray with components travelling in opposite directions.

B.2 Theory
The relative speed of the water affects the speed of light ray passing through it. As the light rays travel in opposite directions with and against the water flow, they move at different speeds, and when recombined they are seen to be out of step with one another – even though their wavelengths are the same.
Altering the water’s flow speed causes the light’s interference fringe pattern to shift.
The refractive index of water, n = 4/3, determines the speed at which light travels through it, c/n. If water then travels at speed through wisp space, it changes the speed at which light travels.
Water molecules create shapes in wisp space that cause light to slow down, and when water moves its shapes displace wisps at right angles to its motion, which affect light’s speed. Moving against the direction of light reduces its speed further, while moving with it reduces the slowing effect and light travels faster.
The process is complex, but it appears that both Einstein’s and Fresnel’s equations do correctly predict the interaction of light with moving water.
Fizeau’s experiment demonstrates that the motion of water speeds up or slows down light. Since the frequency of light leaving the source is the same as that seen by the observer the shift in the observed fringe pattern can only be due to light travelling at different speeds through moving water.

B.3 Applying wisp theory to special relativity’s formula
By applying wisp’s velocity transformations to Einstein’s velocity addition formula we can predict what affect the Earth’s motion through wisp space has on the outcome of the experiment.

Equation set B.1 shows Einstein’s velocity addition formula expressed in terms of wisp’s velocity transformations.
By letting the observer’s speed uobs equal zero (a limit process), the wisp equation reduces exactly to special relativity’s equation, as would be expected (Equation set B.2).

However, when we take into account the Earth’s orbital velocity (its assumed motion through wisp space), it results in a small increase in the time difference interval.
The ratio of wisp time to special relativity time is 1.000265, and it stays constant for varying water speeds (assuming absolute water speeds are small compared to the speed of light).

B.4 Applying wisp theory to Fresnel’s formula
We adapt Fresnel’s formula (Equation set B.4 – upper) to wisp theory by referencing the speed of water to absolute wisp space and adding the effects of time dilation.

Again, when we take into account the Earth’s motion through wisp space, it results in a small increase in the time difference interval (Equation sets B.3 and B.4 lower).

B.5 Conclusion
By applying wisp theory to established equations that appear to give a correct prediction of the speed of light through moving water, we discover that the Earth’s motion causes the time difference term to increase by a small constant multiplying factor of 1.000265.
Equation set B.4 (lower) shows the corrected formula for measurements carried out on Earth (the water’s speed measurement vwater is relative to the Earth’s surface).
By rotating the apparatus such that both arms are perpendicular to the Earth’s motion through wisp space the small offset effect will be cancelled.
It might be possible to detect this offset using sensitive fringe shift detection equipment, and using materials with a higher refractive index – such as glass (refractive index 1.5) – to achieve better accuracy. Glass could be rotated in cylinder form to ensure that its speed is uniformly controlled while the light rays pass through its sides.